Cracking the ZK Prover Network: Unlocking Proofs at Scale with Eigenlayer

^{Guest post by nairolf.}

‍

It's time for the third installation of our “Cracking Lagrange” series. The goal? To explain Lagrange's ideas in simple words so we can all sound smart and understand topics like zero-knowledge proofs and coprocessors. We strongly suggest you check out the first two articles (linked here and here) before jumping into this third one.

If you read our latest piece, you know that Lagrange’s ZK coprocessor lifts intensive computations offchain and generates ZK proofs to verify the results onchain. By doing this, data-heavy workloads become feasible, unlocking a multitude of new use cases and making it possible for developers to build more usable applications that can onboard the next billion users.

All of that sounds quite simple, doesn’t it? Yet one thing remains to be explained: We said that—with Lagrange’s ZK Coprocessor—the computations are moved offchain, then ZK-proofed, and finally sent back onchain. So wait a minute: Who does the proving? It has to be done by someone, right?

That someone is the subject of this third piece. Introducing: Lagrange’s ZK Prover Network!

Defining “ZK Prover Network”

Every application using ZK proofs requires a prover to generate the proofs of its computations. Logical, right? A garage needs a mechanic, a bakery needs a baker, and a shop needs a seller.

While garages, bakeries, and shops may face challenges hiring the right people, developers of ZK applications encounter unique barriers related to ZK, such as complex cryptography or understanding circuits. No need to dive into those details—just know that proving is an extremely complex process.

Until now…

Lagrange’s ZK Prover Network offers reliable proving for various types of complex computations that both developers and protocols can leverage to build more data-rich experiences and enhance the usability of Web3 at large. Think of it as a service specifically designed to produce ZK proofs—essentially, enabling proofs at scale.

How does the Prover Network work? 

First, Lagrange’s ZK Prover Network is made up of two main participants: Gateways and Provers.

In essence, each Gateway connects to one or more Provers within the network and manages a queue of tasks that the Provers commit to complete. Provers are responsible for generating proofs, with tasks distributed according to their workload capacity. This capacity is determined by their stake: the higher the staked amount, the more work they can handle, and consequently, the greater the potential earnings.

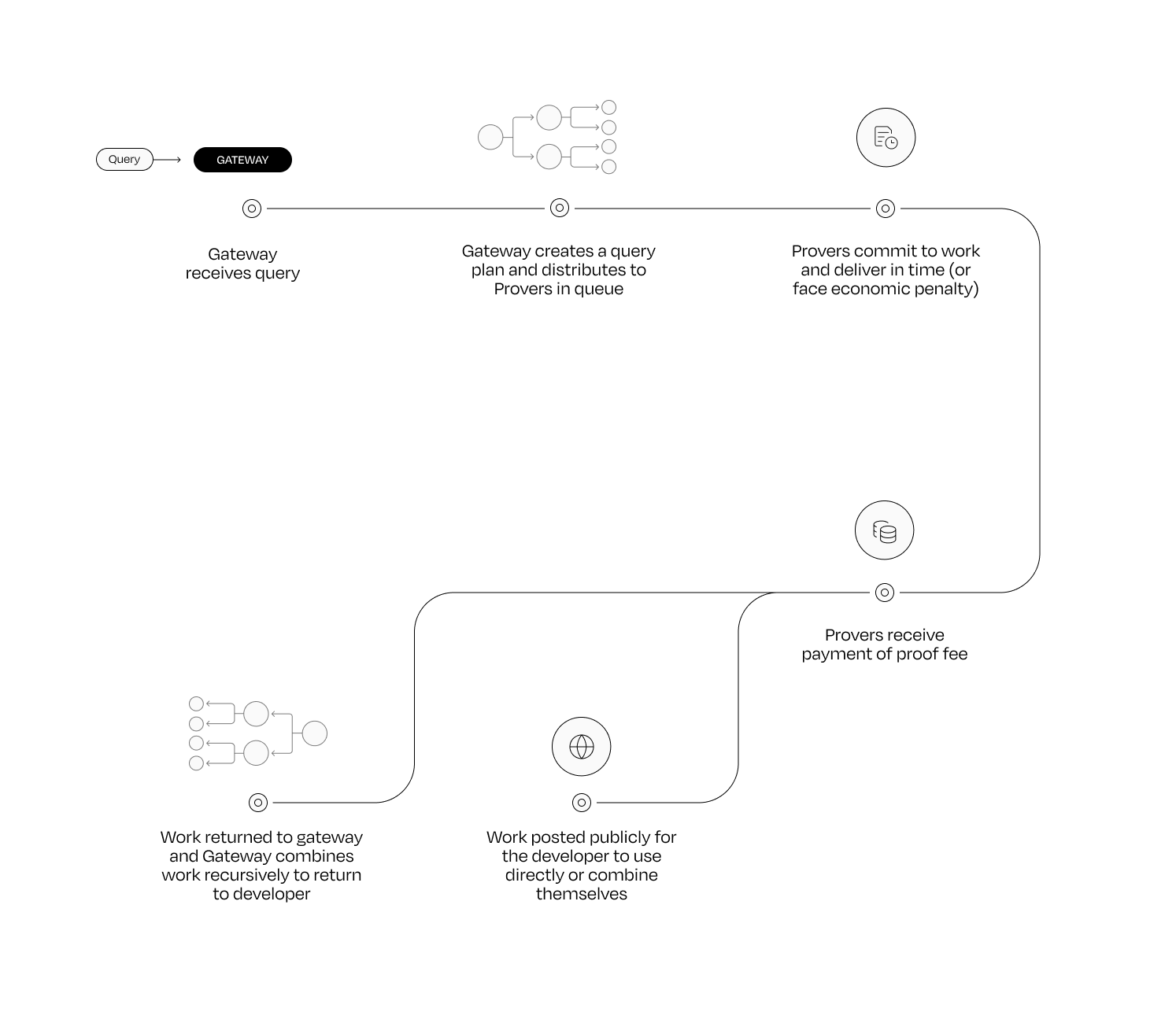
If that sounds confusing, don't worry—that’s what we’re here for! Let’s simplify it: Think of the Lagrange Prover Network as a delivery service, where Gateways act as dispatch centers, and Provers are the delivery drivers.

Gateways (the dispatch centers) receive tasks (orders) from ZK applications and assign them to Provers (delivery drivers) based on each Prover's workload capacity.

Each delivery driver (Prover) has a limit on how many orders they can take (their stake) and commits to completing them on time (generating proofs). If a driver delivers on schedule, they receive payment (rewards). However, if they fail to meet the deadline, they face penalties, similar to a driver losing part of their pay (slashing or non-payment). Put simply, as Eigenlayer’s operators, Provers generate proofs for rewards and put up money as a guarantee that they will do it correctly.

Applications request proof of their computations, Gateways organize the work, and Provers execute it. 

What makes this Prover Network unique? 

As we mentioned earlier, Lagrange’s ZK Prover Network consists of many different Provers, all of which are ready to create ZK proofs whenever needed. This setup reduces the system's dependence on a single Prover, which in turn leads to greater decentralization. By spreading out the work across many Provers, the network becomes more resilient and reliable, ensuring that it can continue functioning smoothly even if one or a few Provers experience issues.

A key advantage of Lagrange’s Prover Network is that it offers clear guarantees about when a proof will be delivered to the blockchain, something that many existing solutions don’t provide. With Lagrange’s Prover Network, operators who run Provers must commit to delivering these proofs within a specific timeframe. To ensure they meet these deadlines, operators are required to pledge a certain amount of capital. If they fail to generate and submit the proof on time, they lose that money or don’t get compensated for the work they have done. This creates a strong incentive for operators to meet their commitments, ensuring that the network remains highly reliable and proofs are delivered on time, giving it high liveness guarantees.

You might now be wondering how this ties into the ZK Coprocessor that we explored in Part 2 of our Cracking Series. The ZK Coprocessor is, in fact, the first proof type deployed on Lagrange's Prover Network. Recall that computations are moved off-chain, zk-proven, and then brought back on-chain. We asked who is responsible for generating these ZK proofs, and now we have the answer: the ZK Prover Network. Because the ZK Prover Network allows Provers to generate various types of proofs, Lagrange was able to innovate the way proofs for the ZK Coprocessor are created, optimizing the process for speed and efficiency. The computational tasks are broken down into many smaller subtasks, which are then proven by the Provers. As a result, Lagrange’s ZK Coprocessor can handle much larger computations and generate proofs much faster than other ZK coprocessors available today.

To sum things up, Lagrange’s ZK Prover Network is a decentralized system that creates proofs. It’s built on EigenLayer and involves two main roles: Gateways and Provers. Gateways organize and assign tasks to Provers, who create the proofs. Provers commit money to ensure they do their job correctly and on time. If they fail, they lose some of that money. While the ZK coprocessor is the first application to use the Prover Network for generating proofs of its calculations, any application can take advantage of the Prover Network for its proving needs. The time when ZK proving was inaccessible is now a thing of the past…

We’ve now cracked three of the main concepts behind Lagrange: zero-knowledge proofs, the ZK Coprocessor and the ZK Prover Network. Stay tuned for the next and final piece in the Cracking series!