Scaling Programmable Trust On EigenLayer With Lagrange’s State Committees and Big Data Coprocessor

A few months ago, we announced plans to create a shared and permissionless zone of security for cross-chain bridging and messaging protocols by combining EigenLayer restaking with Lagrange’s State Committees infrastructure. Lagrange’s State Committees serve as an elegant ZK light client protocol for optimistic rollups. Since then, we have readied the Lagrange State Committees protocol for deployment and are finally close to bringing our AVS to EigenLayer’s testnet and onboarding partner applications.

‍

Ahead of our upcoming AVS deployment, we are releasing a three-part article series to formally introduce Lagrange’s product suite — which includes Lagrange’s State Committees, the Lagrange Coprocessor, and Recproofs/ZK MapReduce — to a broader audience and the developer community. We will dive more into details of each product offering over the course of the series, but you can read some of our previous writings and research for a refresher on Lagrange’s “ZK Big Data stack”:

• Interoperability For Modular Blockchains: The Lagrange Thesis
• A Big Data Primer: Introducing ZK MapReduce
• An Introduction To Lagrange State Committees
• Recproofs: Vector Commitments with Updatable Batch Proofs and their Applications
• Nova: from IVC to general PCD for zkMapReduce

‍

The first article in the series (this post) will touch on Recproofs, ZK MapReduce, and the Lagrange Coprocessor which, when coupled with the Lagrange State Committees infrastructure, can significantly improve expressivity and system performance. Specifically, we will explain how Lagrange’s ZK proving technology powers our State Committees and can enable new design possibilities for AVS teams building on EigenLayer.

Let’s dive in!

‍

State Committees

Current approaches to messaging and bridging between EVM chains rely on partitioned economic security. The security model is typically of the form “kof n” validator honesty assumptions, where proving that a state exists or a transaction occurred on a different chain requires a plurality (k), of a set of total (n) nodes to agree. Examples of these approaches include multi-signature wallets, threshold signatures schemes across attestation sets, Tendermint proof-of-stake consensus and proofs of Ethereum’s light client sync committee. While each of these approaches have distinct advantages, they all share a central design limitation; the vulnerability of small validator quorums. Specifically, each cross-chain protocol has a capped sized set of validators that can be targeted in isolation by compromising a plurality of its nodes, which has occurred in catastrophic fashion in the wild for many bridges.

Lagrange’s State Committees (LSC) are a secure and flexible light client protocol for optimistic rollups. In contrast to isolated “k of n” bridges, the unique attestation mechanism that underpins the cross-chain state committee supports an unbounded set of nodes. As such, the collateral behind each attestation can scale dynamically as more cross-chain protocols decide to pool security into the state committees. This enables the LSC network to exhibit super-linear security, as large pools of capital become exponentially harder to attack at scale than a fragmented sum of their parts.

Lagrange’s State Committees enable a shared economic security hub for interoperability without introducing risk stacking or adding intermediary risk. These features follow immediately from the use of the Lagrange proving stack, as proofs of unbounded sized sets of attestations to blocks can be easily verified on-chain by any contract. Moreover, in the case of Lagrange’s State Committees, the economic security is not limited by the amount of validators, leading to superlinear security, whereby an economic attack on the protocol requires subversion or collusion of the entirety of the economic bandwidth securing State Committees, as opposed to a strictly smaller subset. Since the State Committees are transport layer agnostic, they can be combined additively with the security of existing interoperability protocols. Each proof is lightweight enough that it can be verified anywhere without complex technical overhead.

‍

Scaling verifiable compute and expressivity in the EigenLayer AVS ecosystem

EigenLayer’s programmable trust model — based on ETH restaking — has encouraged developers to rethink approaches to bootstrapping any application that requires distributed validation and consensus (an Actively Validated Service (AVS), as described in the EigenLayer whitepaper). Programmable trust, where on-chain applications can scale economic security dynamically depending on their needs, is a powerful primitive for building a new class of protocols that will power the new Internet of Value.

That said, we see two potential implications of the (inevitable) proliferation of EigenLayer restaking and the associated increases in the number of restaked validators on Ethereum:

1. As EigenLayer middleware infrastructure matures, and key components (e.g., slashing logic) are battle-tested, AVS teams will design for more customizability and have more complex operator requirements as the universe of securable economic transactions expands

2. As AVS deployments increase their operator sets, the need to efficiently perform expressive computations associated with managing EigenLayer operators (e.g., verifying signatures and evaluating operator activity) will grow.

At Lagrange Labs, we are building a set of infrastructure primitives to scale off-chain compute and increase expressiveness of on-chain computation, termed the ZK Big Data Stack. Lagrange Labs’ ZK Big Data Stack is designed to increase the security and expressivity of how contract states can be used on-chain and between chains and comprises:

• Lagrange Coprocessor: A ZK-powered coprocessor designed to lift constraints on developers by providing a cheap environment for executing computation on on-chain data (which would be expensive to execute in a traditional blockchain virtual machine). All state data is derived from on-chain sources — with proofs verifying state access — ensuring that off-chain computation is free of additional trust assumptions.
• ZK MapReduce: A feature of the Lagrange Coprocessor that enables efficient, distributed computation on arbitrary datasets and generation of secure proofs of contract storage. ZK MapReduce improves the Lagrange Coprocessor by overcoming the limitations of sequential-style computation and enabling horizontal scaling through parallel computation and proof generation.
• Recproofs: A vector commitment scheme for concurrently proving both batched set inclusion and dynamic MapReduce-style computations. Recproofs optimize ZK MapReduce computations by enabling recycling of proofs at scale.
• Lagrange’s State Committees: A shared security solution for cross-chain protocols secured by collateral restaked via EigenLayer. The Lagrange State Committees AVS is an elegant ZK light client protocol for optimistic rollups and integrates with the other components of the ZK Big Data Stack for better performance. For example, ZK MapReduce and Recproofs facilitate efficient aggregation of BLS public keys of operators in the Lagrange State Committees AVS and enable higher participation rates in the AVS without increasing overhead of verifying attestations to cross-chain states from operators.

Other AVS teams building applications on EigenLayer can also harness the benefits of scalable, dynamic, and expressive computation provided by Lagrange’s MapReduce Coprocessor, especially the functionality of the Recproofs construction. Specifically, Lagrange’s MapReduce Coprocessor can reduce operational overhead for AVS teams and provide protocol developers with more flexibility in designing custom AVS workflows by enabling:

1. Dynamic and updatable BLS public-key aggregations for AVS node operators
2. Provable queries over EigenLayer Registry contracts from other AVS contracts

In the next sections, we discuss the two aforementioned use-cases of our Recproofs and ZK MapReduce coprocessor in more detail.

‍

Dynamic aggregate BLS public keys for EigenLayer AVS operators

A core component of many AVS deployments on EigenLayer, such as Lagrange’s State Committees, is the verification of a “quorum signature” where a quorum refers to a division of the operator for an AVS deployment. Operators participating in a quorum sign a specific message — these signatures are then aggregated for easy verification using the BLS12–381 primitive — and the AVS protocol decides whether to slash one or more operators depending on certain attributes of the message (e.g., number of signers).

For instance, an AVS can detect operator downtime and slash accordingly by verifying that one or more operators registered for the quorum failed to contribute to the quorum signature. EigenLayer’s registry architecture (we will explain registries in more detail later) is optimized to reduce the cost of verifying quorum signatures. However, signature verification is still relatively expensive — especially since the time and cost of computing an aggregated BLS public key, either on-chain or in circuit, scales linearly with respect to the number of keys that are being aggregated or deaggregated.

For some background, the current approach to BLS signature aggregation and verification on AVS deployments integrated with EigenLayer middleware (e.g., EigenDA) is as follows:

1. When an operator registers for a quorum, their BLS public key is aggregated with the existing aggregated public key (apk) of that quorum to create a new apk.
2. At the time of pre-commitment, the disperser passes the aggregate signature, aggregated public key and non-signer bits on-chain to the checkSignatures function. The checkSignatures function verifies the apk by de-aggregating the non-signers and then checks the validity of the aggregated signature.

With the current flow in mind, we now ask: What if we could improve the BLS signature aggregation and verification workflow to make it cheaper without decreasing soundness?

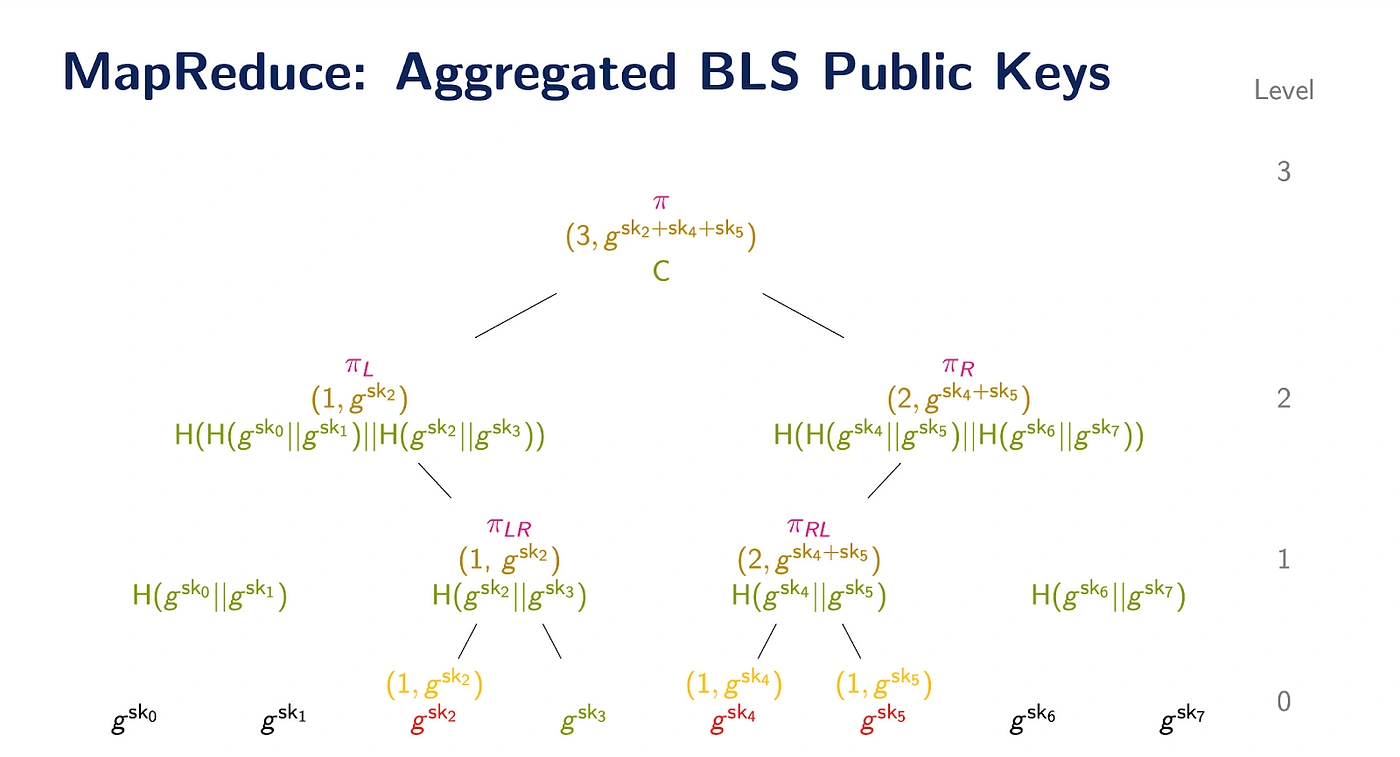
Here, we propose applying Lagrange’s Recproofs and ZK MapReduce coprocessor to improve the efficiency of updating batch proofs of key aggregation in EigenLayer AVS contracts. As mentioned previously, Recproofs is a new vector commitment scheme designed for concurrently proving both batched set inclusion and dynamic MapReduce style computations. Recproofs (in combination with ZK MapReduce coprocessor) is used in Lagrange State Committees AVS to create updatable BLS public key aggregations and allows the AVS operator set to scale to a nearly unbounded size by efficiently computing the aggregated public key.

The premise is that proofs of previous aggregations can be updated (instead of discarded), with the efficiency of the update proportional to the number of signers that have changed in the quorum since the last proof was generated. In contrast to naive approaches, where proving time or gas cost scales linearly with respect to signer or non-signer subset size, using Recproofs means that proving time only scales proportionally to the number of updates required to the signer subset.

Now, using Recproofs, we propose a new approach for BLS Public Key aggregation. Our approach to computing BLS public keys for quorums can be summarized as follows:

When a leaf changes (either in the signer subset or in the overall set), the batch proof can be updated by recomputing only the path that corresponds to the changed element. The proofs for each of the subtrees that were not affected by the change do not have to be recomputed.

Specifically, assume that the BLS public keys of n validators are stored in the memory of some smart contract. With our MapReduce coprocessor we can support creating an updatable public key aggregations with two steps:

1. Generate a proof π of the claim that “apk is the aggregated BLS public key of a subset S of some set of n public keys, that are stored in a Registry contract.”
2. Now suppose we have a message m that was signed by a new subset S’ of validators that is contained in the registry contract. Assume that both S’ ∆ S > 0 and S’ ∩ S > 0. We need to aggregate the keys of a subset S’ of the validators to produce apk’. With Recproofs and our MapReduce coprocessor, instead of generating a new proof π’ from scratch, we can recycle the previously generated proof π efficiently, with updates done in logarithmic time proportional only to S’ ∩ S > 0.

‍

Proving Queries over EigenLayer Registry Contracts

EigenLayer Registries are smart contracts that track certain attributes or meta-properties of individual node operators. The following registry contracts have been built for use by AVSs integrated with EigenLayer’s middleware per the Registries documentation:

• StakeRegistry that keeps track of the stakes of different operators for different quorums at different times
• BLSPubkeyRegistry that keeps track of the aggregate public key of different quorums at different times. Note that the AVS contracts use BLS aggregate signatures due to their favorable scalability to large operator sets.
• IndexRegistry that keeps track of an ordered list of the operators in each quorum at different times.

‍

The data stored in EigenLayer registries is designed to be read from and indexed by actors in an AVS — particularly node operators and AVS coordinators. However, querying registries for operator information can be somewhat costly due to limitations in searching and iterating through mapping types in Solidity.

For context, mappings are not searchable — meaning EigenLayer Registry contracts cannot be efficiently traversed by other on-chain (AVS) contracts — which creates limitations over how data can be queried and used on-chain. To illustrate, it is currently expensive to prove broad queries over on-chain data such as in the EVM (using Solidity) or any other storage proof mechanism, such as:

• “Produce all of the quorums in which address XYZ has participated.”
• “Produce all EigenLayer validators who are participating in protocol X with a stake of an amount greater than Y.”
• “Sum up the weights of all operators who have completed a specific task.”
• “Produce all operators who have not completed a specific task in the past 2 epochs.”

Such queries can be useful for building custom AVS task flows, slashing flows, and payment flows. Additionally, these queries can unlock a wave of innovation by providing new ways for other on-chain applications to compose new functionality on top of EigenLayer. Examples of such logic include automated stake delegation and stake rebalancing based on predefined conditions (e.g., operator participation history, performance, and slashing events).

Lagrange’s Recproofs and ZK MapReduce coprocessor work together to easily alleviate this constraint through creating searchable indexes directly on top of existing on-chain data structures. First, we create a batch proof over the entire portion of the tree corresponding to the mapping or array data structures that we want to search. Since the memory slots of an array or map are typically very close to each other within the MPT tree, our canonical hashing approach saves on duplicate computation.

‍

In order to facilitate cheap state access, Lagrange’s Recproofs can be used to provide efficient Merkle tree digest translation with different hashing functions. Here we have two steps:

1. Optimized Memory Index: To create a searchable index over the contract’s mapping, we first generate a SNARK-friendly data structure (e.g. a Poseidon binary tree) containing all of the elements of the mapping. This requires proving the equivalence between the portion of the MPT storing the Registry mapping and the new data structure.

Specifically, this proof asserts: “The portion of the MPT tree containing nvalues of the mapping can be Merklized with a different SNARK-friendly hash function to create a new digest D’. That is, prove C₁(H₁({a₁, b₁, …, n₁}) == C₂(H₂({a₂, b₂, …, n₂}), so that a₁ == a₂, b₁ == b₂, and so on.”

2. On-Demand Queries: Once the equivalence proof is created for the SNARK-friendly data structure, we can generate proofs for the result of queries from Lagrange’s coprocessor using the optimized root. This enables fast and low-cost on demand queries over the data contained within Registry contracts that can be easily verified on-chain by other contracts.

Moreover, this approach does not require any on-chain caching (which is expensive to maintain and mostly suited for caching block headers). Instead, we effectively just recurse a precomputed proof-of-equivalence into the proof generated for the query. The recursive proof requires ~100ms to verify — and even less with folding schemes implemented — which means that the latency on proving queries is very low (as it always uses the optimized root), but the safety of the proof is always based on the root that is obtained from the block header.

‍

Summary

In this article we outlined how Lagrange’s State Committees, Recproofs and MapReduce coprocessor work together to power new AVS logic and design possibilities on top of EigenLayer. Specifically, we’ve outlined how building on top of EigenLayer’s restaking primitives fundamentally expands the universe of securable financial transactions.

In the next series of articles we’ll be sharing more details and insights on the architecture of Lagrange’s State Committees and further highlight how our MapReduce coprocessor and Recproofs products enable us to generate efficient state proofs for optimistic rollups.

Importantly, developers building interoperability solutions and cross-chain applications — bridges, messaging protocols, cross-chain oracles, and more — will want to stay tuned for our next article, which provides a comprehensive overview of shared security for cross-chain protocols. There, we will explain why shared security is the missing piece in the puzzle of secure interoperability.

For more information on the Lagrange product suite, research, and technical architecture, visit Lagrange Labs website. You can also follow Lagrange on Twitter/X for updates, announcements, and new developments.

‍

What’s next for Lagrange State Committees and MapReduce Coprocessor?

Lagrange Labs’ products and AVS deployment schedule will closely follow that of EigenLayer. For more technical details, see Article II and Article III of this series.

‍

Acknowledgements

Ismael Hishon-Rezaizadeh (Lagrange Labs), Omar Yehia (Lagrange Labs), and Emmanuel Awosika contributed to this article. Emmanuel was contracted by Lagrange Labs to support the writing of this article. We thank the EigenLabs team for their feedback and insight.